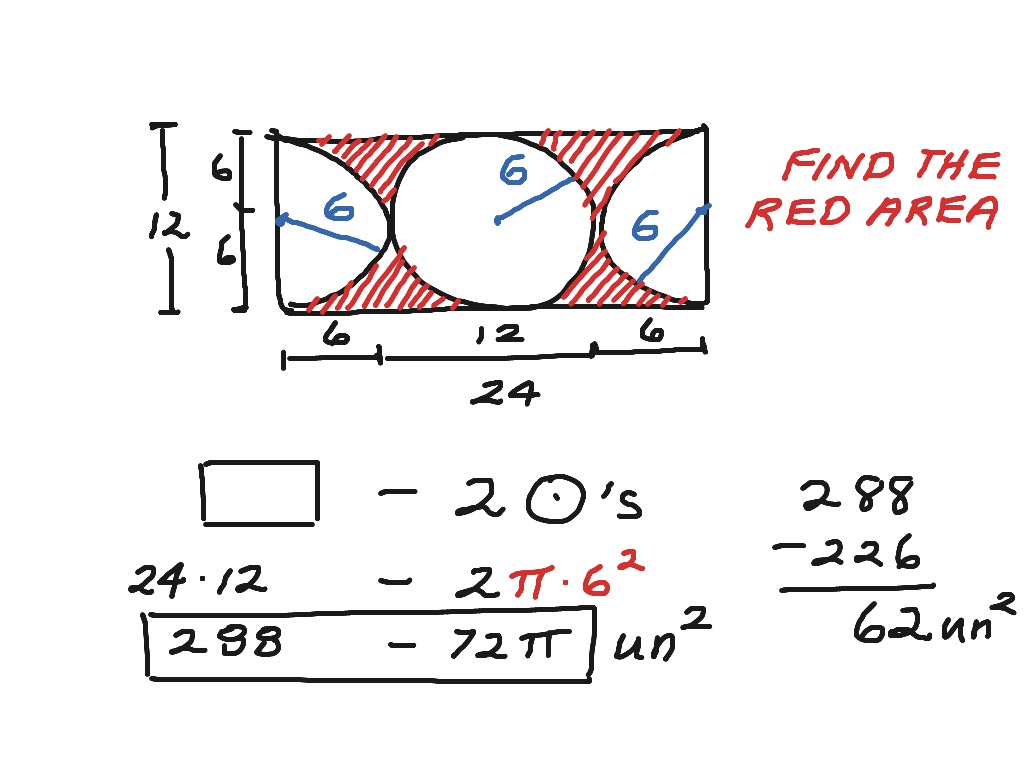
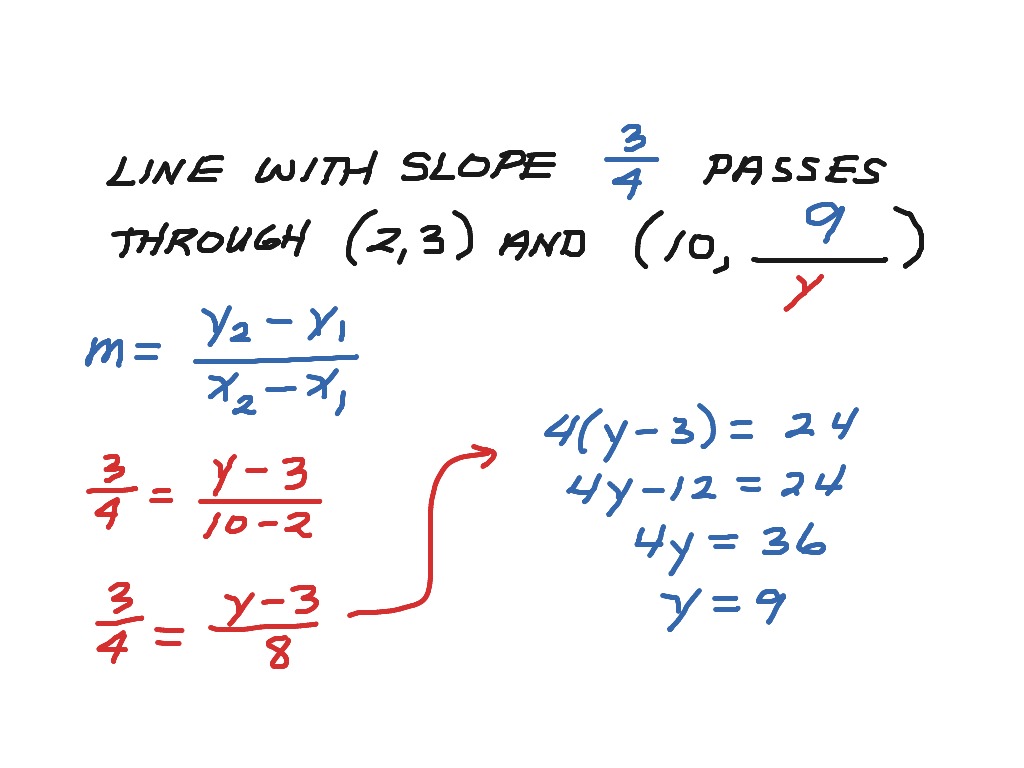
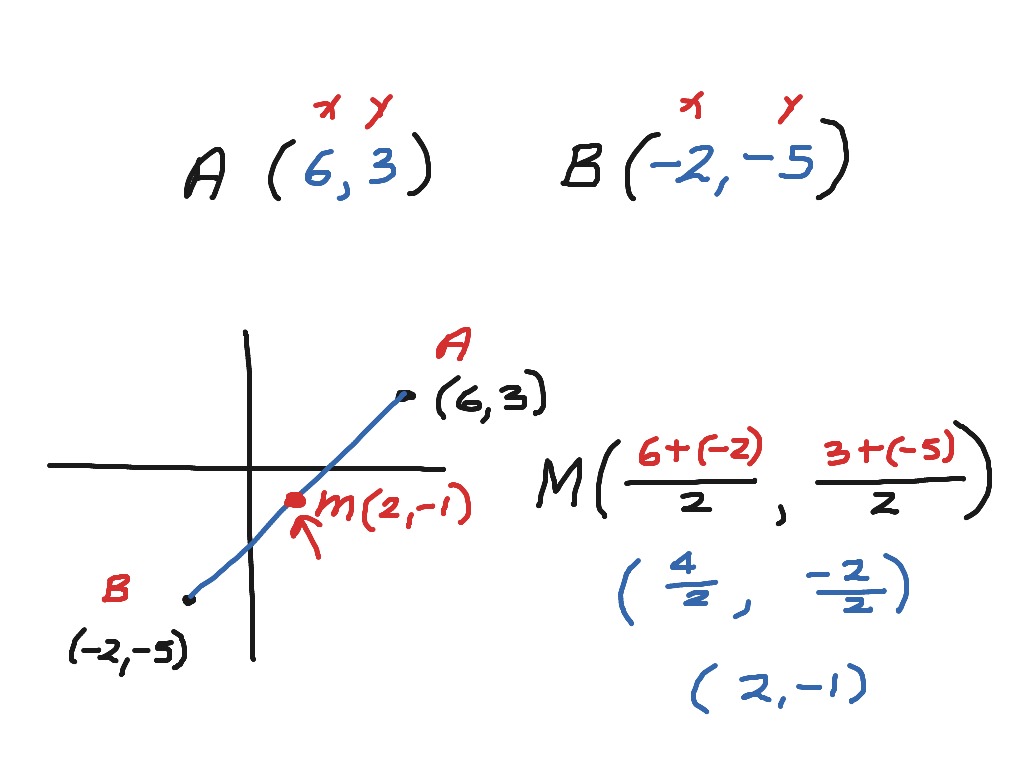Unit 6 Geometry -- Test REVIEW
ann bailey, algebra 1&2, pap...
0
10 years ago
Related ShowMes
0
people liked this ShowMe
Are you sure you want to remove this ShowMe? You should do so only if this ShowMe contains inappropriate content.
Available with ShowMe Premium subscription
Share ShowMe by Email